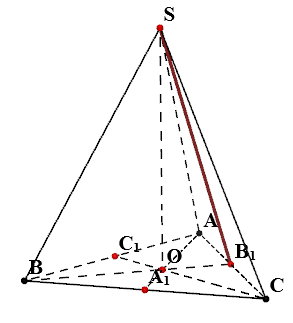
Правильная треугольная пирамида - пирамида, в основании которой лежит правильный треугольник.
Обозначения
- $SABC$ - правильная треугольная пирамида
- $a$ - длина стороны основания пирамиды
- $l$ - длина боковых ребер пирамиды
Площадь основания
В основании правильной пирамиды лежит правильный треугольник со стороной $a$. По свойствам правильного треугольника $$ S_{ABC}=\frac{\sqrt{3}}{4}\cdot a^2 $$Находим $BB_1$
В основании правильной пирамиды лежит правильный треугольник со стороной $a$. По свойствам правильного треугольника $$ AA_1=BB_1=CC_1=\frac{\sqrt{3}}{2}\cdot a $$Находим $BO$ и $OB_1$
По свойствам правильного треугольника $$ AO=BO=CO=\frac{\sqrt{3}}{3} \cdot a$$ С учетом того, что $BB_1=\frac{\sqrt{3}}{2}\cdot a$ $$ OA_1=OB_1=OC_1=AA_1-AO=\frac{\sqrt{3}}{2}\cdot a - \frac{\sqrt{3}}{3} \cdot a=\frac{\sqrt{3}}{6} \cdot a$$Находим $SO$
Из прямоугольного треугольника $BOS$ $$ SO=\sqrt{BS^2-BO^2}=\sqrt{l^2-\frac{1}{3}\cdot a^2} $$ Если $l=a$, то тогда $$ SO=\frac{\sqrt{2}}{\sqrt{3}}\cdot a $$