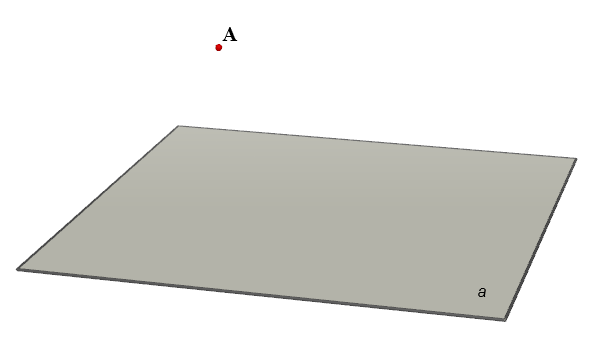
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Опускаем на плоскость $\alpha$ перпендикуляр $AB$ так, чтобы $\angle ABC=\angle ABD=90^{\circ},\ \angle CBD\neq 0$ 
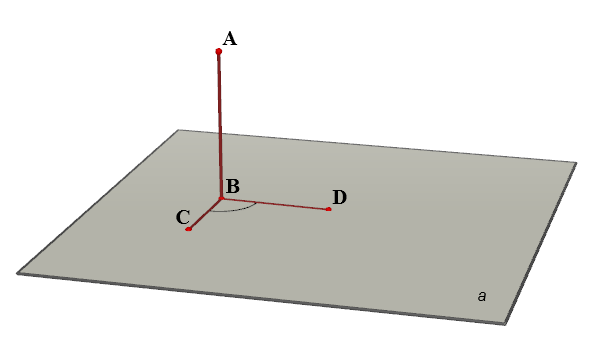Расстоянием между точкой $A$ и плоскостью $\alpha$ будет расстояние $AB$.
Проведем через точку $A$ прямую $AB$, параллельную плоскости $\alpha$. 
Расстоянием между точкой $A$ до плоскостью $\alpha$ будет расстояние между плоскостью $\alpha$ и любой точкой, принадлежащей прямой $AB$. Пример: отметим на прямой $AB$ любую произвольную точку $C$. 
Вне зависимости от того, как мы выбрали точку $C$, расстояние от нее до плоскости $\alpha$ будет равно расстоянию между этой плоскостью $\alpha$ и точкой $A$.
Суть
Если точка лежит на плоскости, расстояние от точки до плоскости считается равным 0. Пусть есть плоскость $\alpha$ и не лежащая на этой плоскости точка $A$. Опускаем на плоскость $\alpha$ перпендикуляр $AB$ так, чтобы $\angle ABC=\angle ABD=90^{\circ},\ \angle CBD\neq 0$ Расстоянием между точкой $A$ и плоскостью $\alpha$ будет расстояние $AB$.
Кроме того
Пусть есть плоскость $\alpha$ и не лежащая на этой плоскости точка $A$. Проведем через точку $A$ прямую $AB$, параллельную плоскости $\alpha$. Расстоянием между точкой $A$ до плоскостью $\alpha$ будет расстояние между плоскостью $\alpha$ и любой точкой, принадлежащей прямой $AB$. Пример: отметим на прямой $AB$ любую произвольную точку $C$. Вне зависимости от того, как мы выбрали точку $C$, расстояние от нее до плоскости $\alpha$ будет равно расстоянию между этой плоскостью $\alpha$ и точкой $A$.